G-Buffer の深度値からワールド空間の位置を復元した秋 2016

2年前の秋に遅延シェーディングのお話をしましたが、あらためて読み返してみたところ、ビュー空間の深度から求めたジオメトリの位置がおかしいことに気づきました¹。今日は、今秋にふさわしい深度の再構築方法 (reconstructing position from depth) について見直していきます。

前回のシェーダー（悪い例）

前回の日記では G-Buffer にビュー空間の深度値を書き込み、必要に応じて深度からライティングパスでポイントライトなどを実装するためには、ワールド空間（またはビュー空間）のジオメトリの位置が必要です。これを G-Buffer の深度値から求めるために次のようにしていました:

// The following code is bad example.
vec3 DepthToPosition(in vec2 textureCoord, in float depth)
{
    vec4 projectedPosition = vec4(textureCoord.xy * vec2(2, -2) + vec2(-1, 1), 0.0, 1.0);

    vec3 viewPosition = (projectionToView * projectedPosition).xyz;
    vec3 viewRay = vec3(viewPosition.xy / projectedPosition.z, 1.0); // maybe bug or typo
    return viewRay * depth;
}

void main()
{
    float viewDepth = DecodeDepth(texture(tex3_DepthSampler, In.TextureCoord.xy).x, FarClip);
    vec3 viewPosition = DepthToPosition(In.TextureCoord.xy, viewDepth);
    vec3 worldPosition = (matrices.ViewToWorld * vec4(viewPosition, 1.0)).xyz;
}

上記の DepthToPosition() の実装を見てみると、 projectedPosition.z で割っているところがあります。ところが projectedPosition の z 値は 0.0 です。常にゼロ除算をしていて、どうみてもジオメトリの位置を求められそうにありません。書いた当時にどうやって式を導出していたのかわからなくなったので、2 年ぶりに G-Buffer のレイアウトも含めて遅延シェーディングを考え直してみます。

G-Buffer

今年の G-Buffer のレイアウトは次のようにしました。

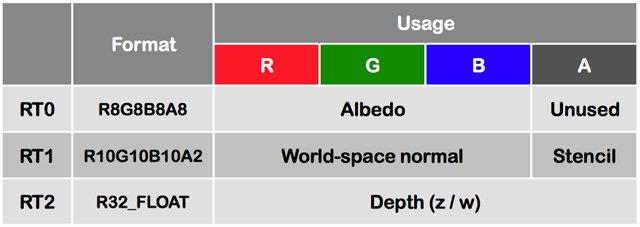
(図 1) G-Buffer のレイアウト

前回の日記とほとんど同じレイアウトです。アルベドは RGB のみ書き込み、RT0 の A 成分は今回未使用です。法線は、ワールド空間の法線を正規化したものを格納しています。一昨年と異なるのは RT1 の A 成分に Stencil を書き込んでいるところです。また RT2 に書き込んだ深度値は、ビュー空間の深度ではなく射影変換後の深度値を書き込んでいます。

このページの後半に実際に書き込んだ G-Buffer のアルベド・法線・深度・ステンシルの各スクリーンショット (図 3) を載せています。

NOTE:
RT0 から RT2 のレンダーターゲットとは別に、デプスステンシルバッファーも利用しています。デプスステンシルバッファーのフォーマットは D24S8 です。今回はこのデプスステンシルバッファーの代わりに、別途レンダーターゲットに書き込んだ深度とステンシル値をその後のライティングパスやポストエフェクトパスで使っています。もちろんデプスステンシルバッファーを利用することでより帯域を節約できます。

定数バッファー

遅延シェーディングのレンダリングパイプラインで共通して使う定数バッファーを先に紹介します。

uniform DeferredShaderParameters {
    mat4x4 ViewProjection;
    mat4x4 InverseView;
    mat4x4 InverseViewProjection;
    mat4x4 TransposedInverseProjection;
} matrices;

ビュー座標変換行列 View と射影変換行列 Projection とするとそれぞれ次のようにして求められます。

mat4x4 ViewProjection = Projection * View;
mat4x4 InverseView = invert(View);
mat4x4 InverseViewProjection = invert(Projection * View);
mat4x4 TransposedInverseProjection = transpose(invert(Projection));

これらの行列をピクセルごとに計算するのはとても大変²なので、事前に CPU 側で計算しておき定数バッファーを経由して各シェーダーに渡すことにします。

法線のエンコードとデコード

法線のエンコードとデコードは前回の日記で紹介したものと同じです。正規化されたワールド空間の法線を G-Buffer に格納します。

vec3 EncodeNormal(in vec3 normal)
{
    return normalize(normal) * 0.5 + 0.5;
}

vec3 DecodeNormal(in vec3 normal)
{
    return normal * 2.0 - 1.0;
}

深度を格納する

G-Buffer を作成するパスの頂点シェーダー

まず頂点シェーダーのコードを載せます。

layout(location = 0) in vec3 Position;
layout(location = 1) in vec3 Normal;
layout(location = 2) in vec2 TextureCoord;

uniform InstancedBlock {
    mat4 LocalToWorld;
} instance;

out VertexData {
    smooth vec3 WolrdNormal;
    smooth vec2 TextureCoord;
    vec2 DepthZW;
} Out;

void main()
{
    vec4 worldPosition = instance.LocalToWorld * Position;
    gl_Position = matrices.ViewProjection * worldPosition;
    Out.WolrdNormal = (mat3x3(instance.LocalToWorld) * Normal.xyz);
    Out.TextureCoord = TextureCoord.xy;
    Out.DepthZW = gl_Position.zw;
}

オブジェクトの頂点シェーダーでは特に難しいことはせず、通常のローカル空間（またはオブジェクト空間²）から射影空間へ変換を行います。

vec4 worldPosition = instance.LocalToWorld * Position;
gl_Position = matrices.ViewProjection * worldPosition;

このとき、射影変換後のオブジェクトの位置 gl_Position の z と w をピクセルシェーダーに出力として渡します。

Out.DepthZW = gl_Position.zw;

G-Buffer を作成するパスのピクセルシェーダー

頂点シェーダーの出力を元に、次のピクセルシェーダーで G-Buffer を作ります。

in VertexData {
    smooth vec3 WolrdNormal;
    smooth vec2 TextureCoord;
    vec2 DepthZW;
} In;

// {xyz_} = Diffuse Albedo RGB (R8G8B8)
// {___w} = Unused (A8)
layout(location = 0) out vec4 AlbedoColorOut;

// {xyz_} = World-space normal (R10G10B10)
// {___w} = Stencil (A2)
layout(location = 1) out vec4 NormalStencilOut;

// {x___} = Depth represented by the formula "z/w" (FP32)
// {_yzw} = Unused
layout(location = 2) out vec4 DepthOut;

uniform sampler2D tex0_AlbedoSampler;

void main()
{
    vec4 textureColor = texture(tex0_AlbedoSampler, In.TextureCoord.xy);
    vec3 normal = EncodeNormal(In.WolrdNormal.xyz);

    AlbedoColorOut = vec4(textureColor.rgb, 1.0);
    NormalStencilOut = vec4(normal.xyz, 1.0);
    DepthOut = vec4(In.DepthZW.x / In.DepthZW.y, 0.0, 0.0, 1.0);
}

深度は、次のように頂点シェーダーで計算した z を w で割ったものを書き出します。

DepthOut = vec4(In.DepthZW.x / In.DepthZW.y, 0.0, 0.0, 1.0);

G-Buffer の深度からワールド空間の位置を求める

作成した G-Buffer の深度からワールド空間のジオメトリの位置を取り出すには、ビュープロジェクション変換の逆行列を使います。次の ReconstructWorldPositionFromDepth() 関数として実装しました。

vec3 ReconstructWorldPositionFromDepth(
    in vec2 textureCoord,
    in float depth,
    in mat4x4 inverseViewProjection)
{
    vec4 projectedPosition = vec4(
        textureCoord.xy * 2.0 - vec2(1.0, 1.0), depth, 1.0);

    vec4 position = inverseViewProjection * projectedPosition;
    return position.xyz / position.w;
}

G-Buffer の UV 空間のサンプリング位置とサンプリングした深度、変換行列の逆行列を使って求めることができます。使い方は次のようにします。

in QuadVertexShaderOutput {
    vec2 TextureCoord;
} In;

uniform sampler2D depthSampler;

void main()
{
    float depth = texture(depthSampler, In.TextureCoord.xy).x;
    vec3 worldPosition = ReconstructWorldPositionFromDepth(
        In.TextureCoord.xy, depth, matrices.InverseViewProjection);
}

ポイントライト

前回の日記では、ディレクショナルライトしか使っていなかったので一切ワールド空間の座標を使っていませんでした。今回は、ポイントライトを実装してジオメトリの位置がちゃんと復元できているか確認しました。

WIP I'll look up how to reconstruct a world position of geometry from depth in deferred shading, instead of using FP32 position buffer pic.twitter.com/PKGrnXomJl
— mogemimi (@mogemimi) September 23, 2016

Screen space shadows using deferred rendering wip pic.twitter.com/q6ZtaHU9BA
— mogemimi (@mogemimi) September 27, 2016

(図 2) ポイントライトを実装してみた動画

ビュー空間の深度か、射影変換後の深度か

前回の日記で、なぜ射影変換後の深度ではなくビュー空間の深度を G-Buffer に書き込んでいたのかというと SSAO で利用したかったからです。 SSAO の実装方法にもよりますが、僕が試してみたところ、頂点シェーダーから書き出される通常の深度値 (射影空間の z を w で割ったもの) よりもビュー空間の z 値を利用したほうが綺麗な AO を計算できました。今回は、射影変換後の深度を G-Buffer に書き込みます。そこで SSAO の計算をするときに射影変換後の深度からビュー空間の深度へ再構築する必要があります。

NOTE:
これといって深度の精度などは考えず、 G-Buffer を 32-bit の浮動小数点にし、 z/w を書き込むように今回はしてみましたが、ひとえに 深度 (depth) といっても G-Buffer に格納する深度は実装によって様々です。フォーマットも 16-bit, 24-bit, 32-bit が選択できますし、対数 (logarithmic) だけでなく線形 (linear) の深度計算方法³も知られています。また、広大な世界を表現するために、できるだけ遠くにあるジオメトリの深度まで表現したいものです。参考文献に載せたページで紹介されている Reversed-Z mapping や Near-far swapped と呼ばれるテクニックがこれに該当します。最新の Unity 5.5 でも Reversed-Z が活用されているそうです。

G-Buffer の z/w 深度からビュー空間の深度を求める

G-Buffer に書き込んだ深度から SSAO で利用するビュー空間の深度を求めます。ワールド空間の位置を求めたときと同じ手順です。今度はビュー空間の深度（または、位置の z 成分）を求めたいので、射影変換の逆行列を用います。

float ReconstructViewSpaceDepthFromProjectionDepth(
    in float depth,
    in vec2 textureCoord,
    in mat4x4 inverseProjection)
{
    vec4 projectedPosition = vec4(
        textureCoord.xy * 2.0 - vec2(1.0, 1.0), depth, 1.0);

    vec4 position = inverseProjection * projectedPosition;
    vec3 viewSpacePosition = position.xyz / position.w;
    return viewSpacePosition.z;
}

position の z と w 成分さえわかれば良いので、次のように行列とベクトルの積を各列と行のベクトルの内積 (dot) で置き換えることもできます。 GLSL で行列の列ベクトルにアクセスしやすくするため射影変換の逆行列を転置しています。

float ReconstructViewSpaceDepthFromProjectionDepth(
    in float depth,
    in vec2 textureCoord,
    in mat4x4 inverseProjection)
{
    vec4 projectedPosition = vec4(
        textureCoord.xy * 2.0 - vec2(1.0, 1.0), depth, 1.0);

    mat4x4 transposedInverseProjection = transpose(inverseProjection);
    float z = dot(transposedInverseProjection[2], projectedPosition);
    float w = dot(transposedInverseProjection[3], projectedPosition);
    return z / w;
}

あらかじめ転置(transpose)しておいた行列を定数バッファにいれておき、関数のパラメータとして渡すようにしました。次の関数でビュー空間の深度を求めます。

float ReconstructViewSpaceDepthFromProjectionDepth(
    in float depth,
    in vec2 textureCoord,
    in mat4x4 transposedInverseProjection)
{
    vec4 projectedPosition = vec4(
        textureCoord.xy * 2.0 - vec2(1.0, 1.0), depth, 1.0);

    float z = dot(transposedInverseProjection[2], projectedPosition);
    float w = dot(transposedInverseProjection[3], projectedPosition);
    return z / w;
}

使い方は次の通りです。

uniform sampler2D depthSampler;

void main()
{
    float depth = texture(depthSampler, In.TextureCoord.xy).x;

    float viewSpaceDepth = ReconstructViewSpaceDepthFromProjectionDepth(
        depth, In.TextureCoord.xy, matrices.TransposedInverseProjection);
}

G-Buffer の可視化と Linear Depth (線形な深度値)

G-Buffer のスクリーンショットを図 3 に示します。

(図 3) G-Buffer の内容を可視化したもの。上から (A) アルベド, (B) ワールド空間の法線, (C) 深度（実際は z/w の値を書き込んでいるが可視化するためにここでは線形な深度に変換してから表示している）, (D) ステンシル

法線は正規化された 3 次元のベクトルで x, y, z の各成分は -1.0f から 1.0f の値をとります。 G-Buffer に格納する際に 0.0f から 1.0f の範囲におさまるようエンコードするため、図 3 のようにワールド空間の法線を RGB の色として可視化できました。ところが z/w で計算される深度バッファーは浮動小数点で 0.0f から 1.0f の範囲内に収まるとはかぎりません。

深度バッファーを図 3 のように色の明暗で可視化するためには、 0.0f から 1.0f の範囲に深度をエンコードする必要があります。深度のエンコード方法のひとつに Linear Depth や Linearized Depth というテクニック³があります。実際に図 3 の深度バッファーのスクリーンショットは、この Linear Depth を使用して撮影しています。次のシェーダーコードを用いました。

float LinearizeDepth(float depth, float near, float far)
{
    return (2.0 * near) / (far + near - depth * (far - near));
}

uniform sampler2D depthSampler;

void main()
{
    float depth = texture(depthSampler, In.TextureCoord.xy).x;
    float linearZ = LinearizeDepth(depth, NearClip, FarClip);
    FragColor = vec4(vec3(linearZ), 1.0);
}

スクリーンショット

SSAO (Screen Space Ambient Occlusion)

今年も SSAO のお世話になっています。一昨年の日記から改良を加えており、綺麗な AO に近づいたと思います (図 4 参照) 。サンプリング数は 1 ピクセルにつき 12 回 (= 6 個のベクトル × 左右 1 回ずつのサンプリング) です。サンプリング半径を大きくすると、粗が目立つ欠点はありますが柔らかい自然な影になります (図 5 参照) 。反対にサンプリング半径を小さくすると、くっきりとした影が表現できます (図 6 参照) 。そうして深度をサンプリングして計算した AO (図 5, 6 参照) に、最終的にブラーをかけたものが図 4 になります。深度値を使って垂直方向と水平方向にわけてバイラテラルフィルターでブラーをかけています。

(図 4) SSAO で計算した AO 影

(図 5) ブラーをかける前の AO

(図 6) サンプリング半径を小さくした例。上から (A)サンプリング半径を図 5 の半分にしたもの, (B) サンプリング半径を可能なかぎり小さくしたもの

ハードウェアインスタンシング

一昨年と同じように、ハードウェアインスタンシングでたくさんのボクセルを表示しています。一昨年は 6 面からなる正立方体の頂点列を元にインスタンシングしていましたが、今回はサーフェイス（ポリゴンを 2 つ組み合わせた正方形の面）をインスタンシングすることにしました。ワイヤーフレーム表示するとよくわかるかと思います (図 7 参照) 。 2013 年の日記ではボクセルをそのままインスタンシングしたものをワイヤーフレーム表示しているのでぜひ見比べてみてください。

(図 7) ワイヤーフレーム表示した例。ワイヤーフレームのために背面カリングを無効にしているが、実際にポリゴンで表示するときは反時計回りの頂点列に対して背面カリングをしている

大気散乱シミュレーション

背景がコーンフラワーブルーで悲しかったので、レイリー散乱とミー散乱をピクセルシェーダーで計算した大気散乱シミュレーションをしてみました。半球状のポリゴンなどは用意せずに、半球やレイの衝突などの計算はすべてスクリーンスペースのピクセルシェーダー上でやっています (図 8 参照)。ディレクショナルライトの向きを半球状の太陽の軌道と捉えて、昼から夜までの天体を表現できます（図 9 参照）。

サンプル数を増やすと SSAO や FXAA の比ではないほどに重たくなるので 1/8 サイズのレンダリングターゲットで計算して、リニアサンプラーで最終的に合成しています。スクリーンスペースのシェーダーなので地面を向いているときも全画面で計算されてしまいます。半球ドームのポリゴンを用意して Z pre-pass の恩恵を受けたり、可能なら頂点シェーダーで散乱のシミュレーションをやってみてもいいかもしれません。大気散乱シミュレーションについては機会があったら日記に書こうと思います。

(図 8) 背景のレンダリング。ピクセルシェーダーで大気散乱シミュレーションをしている。

(図 9) 夕暮れ時の表現。太陽の位置を変えることで昼から夜まで表現できる。

コンポジションとポストエフェクト

図 10 はディレクショナルライトでランバートライティングしたものです。これに SSAO のパスで計算しておいた AO をライティングパスの段階で付け足し (図 11 参照)、ポストエフェクトとして FXAA （図 12 参照）、Exponential Fog （図 13 参照）を順に適用し、被写界深度ブラーをかけて最終的なレンダリング結果となります（図 14 参照）。

(図 10) ディレクショナルライトによるライティング結果。SSAO と FXAA が無効になっている。

(図 11) SSAO を有効にしたライティング

(図 12) FXAA を有効にしたスクリーンショット

(図 13) Exponential Fog を有効にしたスクリーンショット

(図 14) 被写界深度ブラーをかけた、最終的なレンダリング結果

参考文献

Maximizing Depth Buffer Range and Precision - 深度バッファーで表現できる範囲とその精度を最大化する考察記事です。 16 bit/24 bit でも十分な範囲の深度を格納するテクニックが考察されています。
Depth Precision Visualized - NVIDIA GameWorks のブログ記事。深度の精度を目に見えるグラフにして Reversed-Z mapping などを考察しています。

Lee Hyukjae (@namoeye) さんから教えていただき気づきました。ありがとうございます！ Thank you @namoeye for pointing out! ↩
Autodesk Maya だとオブジェクト空間とローカル空間は厳密に言葉の定義がされていて、この場合だとオブジェクト空間というのがふさわしいです。Houdini だとローカル空間で統一されているようです。 ↩
深度バッファーを可視化するために Linear Depth を紹介している次の記事を参考にしました。 [GeeXLab] How to Visualize the Depth Buffer in GLSL ↩

Engine Trouble